Let's Build a Simple Database
제7 장 - B-트리 소개

이 글은 Connor Stack의 Let’s Build a Simple Database를 번역한 글입니다.

알림 : 부족한 실력 탓에 잘못된 번역, 부자연스러운 문장이 있을 수 있습니다. 해당 문제에 대한 의견을 댓글이나 GitHub 저장소 Pull Request를 통해 제안해 주시면 감사한 마음으로 적극 반영하도록 하겠습니다. 감사합니다.

• 제1 장 - 소개 및 REPL 구축
• 제2 장 - 세상에서 가장 간단한 SQL 컴파일러 및 가상 머신
• 제3 장 - 메모리 내, 추가 전용, 단일 테이블 데이터베이스
• 제4 장 - 첫 테스트 (그리고 버그)
• 제5 장 - 디스크 지속성
• 제6 장 - 커서 추상화
• 제7 장 - B-트리 소개
• 제8 장 - B-트리 단말 노드 형식
• 제9 장 - 이진 탐색 및 중복 키
• 제10 장 - 단말 노드 분할
• 제11 장 - B-트리 재귀 탐색
• 제12 장 - 다중 레벨 B-Tree 순회
• 제13 장 - 분할 후 부모 노드 갱신

---

B-트리는 SQLite가 테이블과 인덱스를 표현할 때 사용하는 데이터 구조로써, 매우 핵심적인 개념입니다. 이번 장에서는 오직 데이터 구조에 대해 소개하며, 코드 관련 내용은 없습니다.

왜 트리가 데이터베이스에 적합한 데이터 구조일까요? 답은 다음과 같습니다.

• 특정 값을 탐색하는 속도가 빠릅니다. (로그 시간)
• 찾은 값에 대해서 삽입 / 삭제하는 것이 빠릅니다. (다시 균형을 찾는데 거의 상수 시간)
• 일정 값의 범위를 순회하는 것이 빠릅니다. (해시 맵과는 달리)

B-트리는 이진 트리와는 다릅니다. (“B”는 고안자 이름을 뜻하지만, “balanced(균형)”의 의미도 있습니다.) B-트리의 예는 다음과 같습니다.

B-트리 예 (https://en.wikipedia.org/wiki/File:B-tree.svg)

이진 트리와는 달리, B-트리의 각 노드는 두 개 이상의 자식 노드를 가질 수 있습니다. 각 노드는 최대 m 개의 자식 노드를 가지며, m 은 트리의 “차수(order)” 라고 부릅니다. 트리의 균형을 유지하기 위해, 노드들은 적어도 m/2 (반올림) 개의 자식 노드를 가져야 합니다.

예외:

• 단말 노드는 자식 노드를 갖지 않습니다.
• 루트 노드는 m 개 보다 작은 자식을 가질 수 있지만 반드시 2개 이상이어야 합니다.
• 루트 노드가 단말 노드인 경우 (유일 노드), 자식 노드를 갖지 않습니다.

위의 그림은 SQLite가 인덱스 저장에 사용하는 B-트리입니다. 테이블 저장에는 B+ 트리라는 변형 자료구조를 사용합니다.

	B-트리	B+ 트리
발음	“비 트리”	“비 플러스 트리”
사용하여 저장하는 것	인덱스	테이블
내부 노드의 키 저장 유무	예	예
내부 노드의 값 저장 유무	예	아니오
각 노드 별 자식 노드 수	적음	많음
내부 노드 vs. 단말 노드	동일 구조	다른 구조

인덱스를 구현하기 전까지는 B+ 트리에 대해서만 이야기하지만, 편의상 B-트리로 부르겠습니다.

자식을 갖는 노드를 “내부(internal)” 노드라고 합니다. 내부 노드와 단말 노드는 다른 구조를 갖습니다.

m 차수 트리의 경우…	내부 노드(Internal Node)	단말 노드(Leaf Node)
저장하는 것	키와 자식 노드 포인터	키와 값
키의 개수	최대 m-1 개	저장할 수 있는 만큼
포인터의 개수	키의 개수 + 1 개	없음
값의 개수	없음	키의 개수
키의 목적	탐색에 사용	값과 짝을 이룸
값 저장 유무	아니오	예

예제를 통해 원소가 삽입될 때 B 트리가 어떻게 자라는지 보겠습니다. 간단한 설명을 위해 트리의 차수는 3으로 설정하겠습니다. 차수가 3인 트리는 다음과 같습니다.

• 내부 노드는 최대 3개의 자식 노드를 갖습니다.
• 내부 노드는 최대 2개의 키를 갖습니다.
• 내부 노드는 적어도 2개의 자식 노드를 갖습니다.
• 내부 노드는 적어도 1개 이상의 키를 갖습니다.

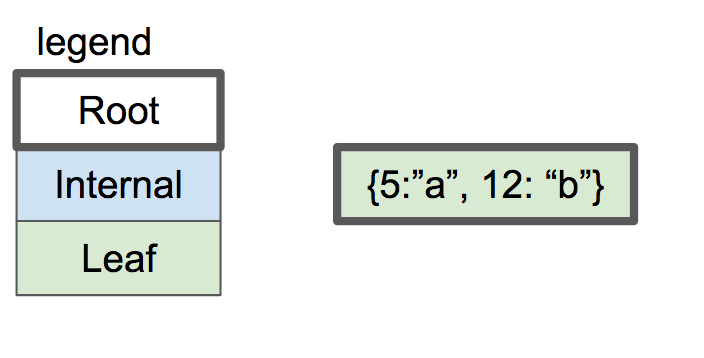
빈 B-트리는 루트 노드라는 단일 노드를 갖습니다. 루트 노드는 키/값 쌍의 개수가 0인 단말 노드로 시작합니다.

빈 B-트리

두 개의 키/값 쌍을 삽입하면, 정렬된 순서대로 단말 노드에 저장됩니다.

단일 노드 B-트리

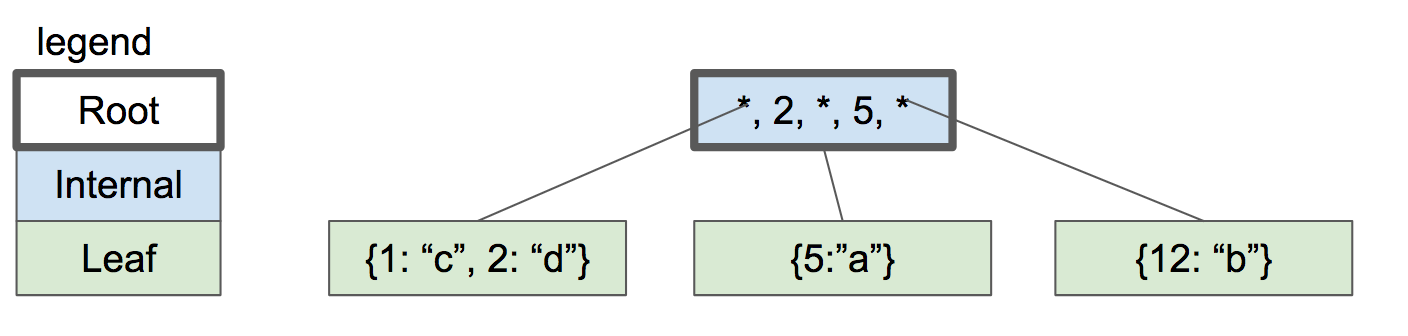
단말 노드의 용량이 두 개의 키/값 쌍이라고 해보겠습니다. 여기서 또 다른 원소를 삽입하는 경우, 단말 노드를 분할하고 각 노드로 키/값 쌍을 절반 씩 나눕니다. 분할로 생성된 두 개의 노드는 새로운 내부 노드의 자식이 되고, 내부 노드는 루트 노드가 됩니다.

레벨 2 B-트리

내부 노드에는 키 1개와 자식 노드에 대한 2개의 포인터가 있습니다. 만약 5보다 작거나 같은 키를 탐색하는 경우, 왼쪽 자식 노드를 탐색합니다. 반대로 5보다 큰 키를 탐색하는 경우 오른쪽 자식 노드를 탐색합니다.

이제 “2”번 키를 삽입해보겠습니다. 먼저 키가 존재한다면 위치해 있을 단말 노드를 찾기 시작합니다. 그렇게 왼쪽 단말 노드에 도착하게 됩니다. 해당 노드가 가득 찼으므로, 리프 노드를 분할하고 부모 노드에 새로운 가지를 만듭니다.

4개 노드를 갖는 B-트리

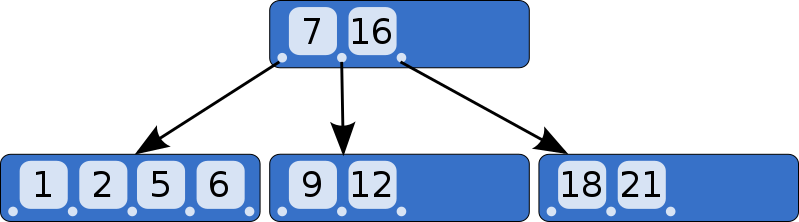
계속해서 키를 추가하겠습니다. 추가할 키는 18과 21번입니다. 다시 분할이 필요한 지점에 생겼습니다. 하지만 부모 노드에 다른 키/포인터 쌍을 위한 공간이 없습니다.

단말 노드가 꽉찬 경우

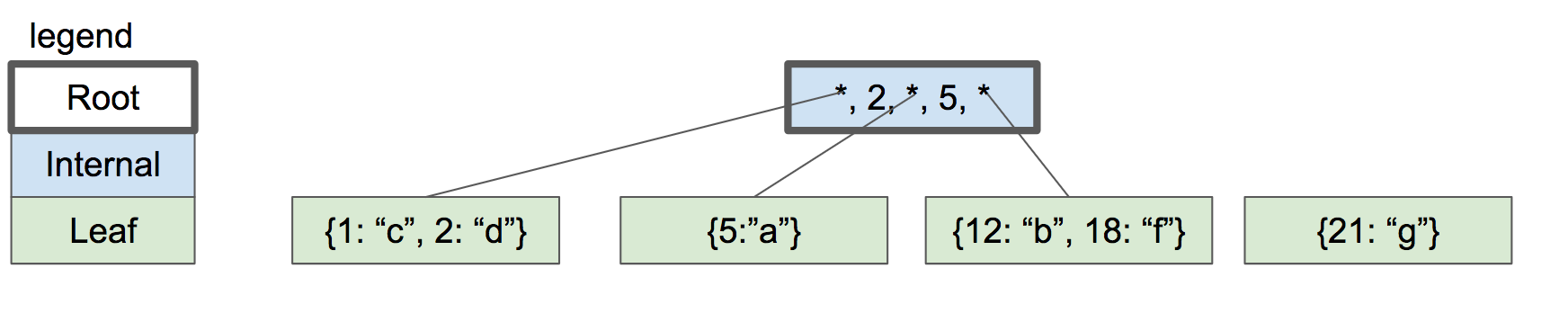해결 방법은 루트 노드를 두 개의 내부 노드로 분할하고, 내부 노드의 부모 노드로 새로운 루트 노드를 생성하는 것입니다.

레벨 3 B-트리

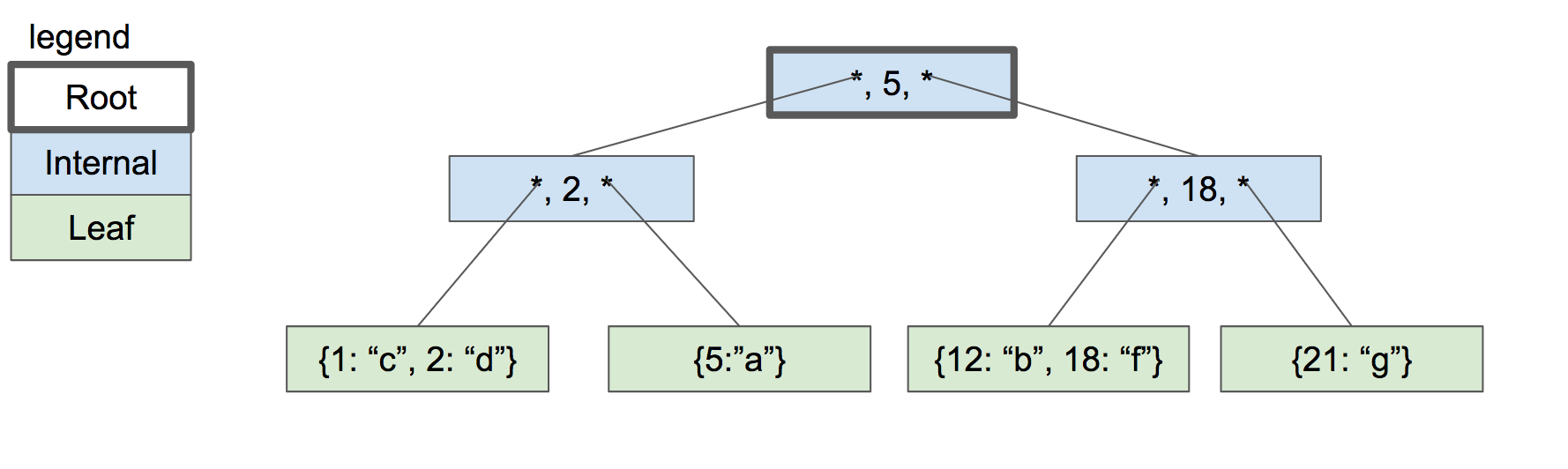B-트리의 깊이는 루트 노드를 분할할 때만 증가합니다. 이를 통해, 모든 단말 노드는 같은 깊이와 비슷한 수의 키/값 쌍을 갖습니다. 따라서, 트리는 균형을 유지하며 빠른 탐색을 가능케 합니다.

B-트리에서 키를 삭제하는 것은 삽입을 구현한 후 다루도록 하겠습니다.

B-트리 데이터 구조를 구현하면 각 노드는 한 페이지에 해당됩니다. 루트 노드는 0번 페이지에 해당됩니다. 자식 노드 포인터는 자식 노드에 해당하는 페이지 번호를 저장하는 것으로 간단하게 구현될 것입니다.

다음 장에서 B-트리 구현을 시작하겠습니다!